Unity Poradnik – krótki wpis rozwiązujący konkretny problem w Unity.
Dzisiejszy odcinek: Praca z krzywymi Béziera w Unity
Jest to kolejny wpis który zawdzięczacie osobie trzeciej. Tym razem gościnnie zawitał do nas Jakub, który chciał wam przybliżyć temat Krzywych Beziera, czyli będzie nieco trudniej i nieco bardziej matematycznie. Bawcie się dobrze.
Wstęp
Krzywe Béziera są powszechnie stosowane między innymi w grafice komputerowej. W
grach znajdą zastosowanie np. przy tworzeniu dróg, rzek, wytyczania trasy dla AI, czy
przy tworzeniu UI.
Krzywe Béziera dzielą się na krzywe wielomianowe i krzywe wymierne. W tym wpisie będziemy pracować na krzywych wielomianowych. Krzywą Béziera definiuje się za pomocą zestawu punktów kontrolnych P0 do Pn. Pierwszy i ostatni punkt to punkty początku i końca krzywej. W praktyce wykorzystuje się krzywe niskich stopni, opisywane niewielką liczbą punktów kontrolnych. Najczęściej za pomocą trzech (krzywe kwadratowe) lub czterech (krzywe sześcienne) punktów kontrolnych.
Aby narysować taką krzywą na ekranie musimy obliczyć punkty znajdujące się na krzywej a
następnie należy je połączyć prostymi odcinkami. Kształt krzywej kontrolujemy za pomocą odpowiedniego ułożenia punktów kontrolnych.
[stextbox id=’info’ defcaption=”true”]Zarówno krzywe wielomianowe, jak i wymierne cechuje jedna wspólna niedogodność – trudno za pomocą jednej krzywej przedstawiać skomplikowane kształty. Z tego względu powszechnie stosuje się krzywe B-sklejane, które oferują lokalną kontrolę kształtu.[/stextbox]
Teoria:
Do obliczenia punktu na krzywej będą nam potrzebne współrzędne punktów kontrolnych oraz parametr t, który mieści się w przedziale od 0 do 1 określający, w którym miejscu krzywej znajduje się szukany punkt.
Liniowe krzywe Béziera
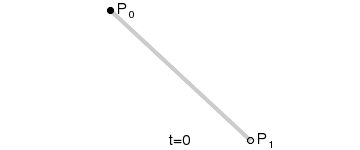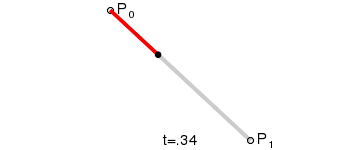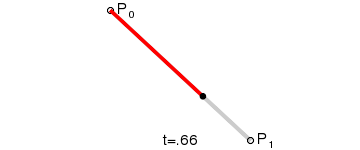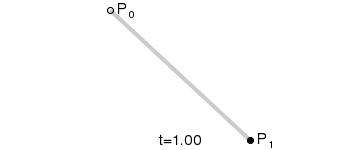
Mając punkty P0 oraz P1, liniowa krzywa Béziera jest odcinkiem pomiędzy nimi. Krzywa podana jest wzorem: B(t) = P0 + t(P1 – P0) = (1 – t)P0 + tP1 , t ∈ [0,1] i odpowiada interpolacji liniowej.
Kwadratowe krzywe Béziera
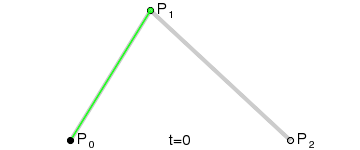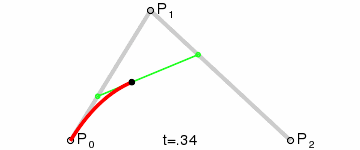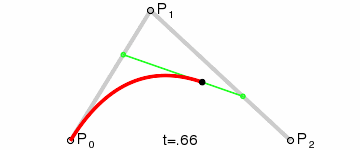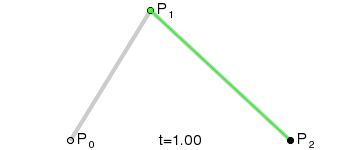
Źródło: wikimedia.org
Kwadratową krzywą Béziera otrzymamy kreśląc funkcję B(t), mając punkty P0 ,P1 oraz P2. Uproszczona wersja funkcji to: B(t) = (1 -t)2P0 + 2(1 – t)tP1 + t2P2 , t ∈ [0,1]
Sześcienne krzywe Béziera
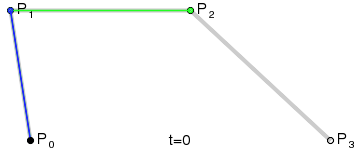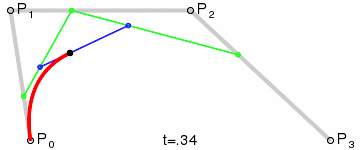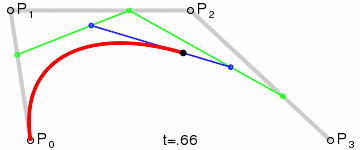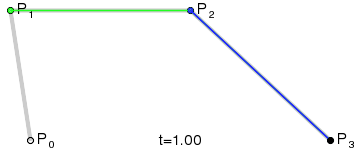
Źródło: wikimedia.org
Cztery punkty P0 ,P1 ,P2 oraz P3 definiują sześcienną krzywą Béziera. Uproszczona wersja funkcji to: B(t) = (1 -t)3P0 + 3(1 – t)2tP1 + 3(1 – t)t2P2 + t3P3 , t ∈ [0,1]
Praktyka
Poznaliśmy już w jaki sposób możemy wyliczyć punkt na krzywej, więc pora odpalić Unity i
zabrać się za praktykę. Przykład będzie przedstawiał sposób implementacji sześciennej krzywej Béziera oraz jej wizualizację za pomocą komponentu LineRenderer.
Na początku dodajemy do sceny pusty obiekt typu Empty, który posłuży nam jako pojemnik
na skrypt. Następnie tworzymy skrypt o nazwie krzywaBeziera.cs i przypisujemy ten skrypt do obiektu
typu Empty, który wcześniej dodaliśmy do sceny.
Przechodzimy do edycji naszego pliku ze skryptem. Na początek dodajemy sobie kilka zmiennych:
using UnityEngine;
using System.Collections.Generic;
[RequireComponent(typeof(LineRenderer))]
public class krzywaBeziera : MonoBehaviour
{
public LineRenderer lineRenderer;
public Vector3[] punktyKontrolne;
[Range(2, 50)]
public int gladkoscKrzywej = 50;
private Vector3[] vP = new Vector3[gladkoscKrzywej];
}Atrybut RequireComponent dodany tuż przed deklaracją klasy zapewnia automatycznie dodanie komponentu. Zmienna punktyKontrolne posłuży nam do przechowywania punktów kontrolnych krzywej. punkty te podajemy w inspektorze. Kolejne pole to gladkoscKrzywej – określa ono ile punktów kontrolnych chcemy użyć do narysowania krzywej. Tablica vP posłuży nam do przechowywania punktów znajdujących się na krzywej, które zostały wyliczone według wzoru.
Kolejny fragment kodu to metoda Start.
void Start()
{
if (!lineRenderer) {
lineRenderer = GetComponent<LineRenderer>();
}
}Przypisujenu tu komponent LineRenderer jeśli zmienna lineRenderer jest pusta.
Teraz przejdźmy do metody Update:
void Update()
{
lineRenderer.positionCount = vP.Length;
float t = 0f;
for (int i = 1; i <= gladkoscKrzywej; i++) {
Vector3 punkt = PunktNaKrzywej(t, punktyKontrolne[0], punktyKontrolne[1],
punktyKontrolne[2], punktyKontrolne[3]);
vP[i-1] = punkt;
t += 1/((float)gladkoscKrzywej-1)
}
lineRenderer.SetPositions(vP);
}Do positionCount przypisujemy liczbę punktów kontrolnych. Następnie dodajemy pętlę, która
wykona tyle obiegów ile jest punktów kontrolnych. Co obieg zostaje wywoływana metoda PunktNaKrzywej. Zwraca nam ona punkt na krzywej, który zapisujemy sobie do tablicy vP. Na koniec przekazujemy tablicę punktów do SetPositions. Zmienna t, to nic innego jak parametr t z podanych wcześniej wzorów, potrzebny do obliczenia pozycji punktów.
Na koniec zostaje nam do dodania metoda o nazwie PunktNaKrzywej, która jest
odpowiedzialna za… wyliczenie punktu na krzywej. Jest to praktycznie najważniejsza część
naszego kodu.
PunktNaKrzywej(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
{
Vector3 p = (1-t)*(1- t)*(1-t)*p0+3*(1- t)*(1-t)*t*p1+3*(1- t)*t*t*p2+t*t*t*p3;
return p;
}Na koniec pozostaje wprowadzić dane do inspektora. A dokładniej do listy punktyKontrolne. Ja proponuję wpisać następujące współrzędne:
- 0, 0, 0
- 0, 20, 0
- 20, 20, 0
- 20, 0, 0.
Po co nam to wszystko? W ten sposób narysowaliśmy w zasadzie linię. Ale możemy ten sam sposób wykorzystać do narysowania rzeki czy drogi, kiedy generujemy nasz świat proceduralnie. Można też wykorzystać tą metodę do generowania drogi dla AI, jeśli standardowy NavMesh wam się nie podoba.